The task: to apply pattern recognition to images of objects.
Pattern recognition is basically deciding whether a given feature vector (an ordered set of a quantifiable property, features that make up a pattern, such as color, shape, size, etc.) belongs to one of several classes (a set of patterns that share a common property).
Procedure:
**A set of objects are assembled that may be classified into 2 to 5 classes, with 10 samples for each class. Half serves as a training set, while the other half serves as a test set.
[Photo]
**Images of these objects are captured while features are chosen and extracted from them. These features are then separated into test feature vectors and training feature vectors.
Here we choose:
**The training feature vectors are then used to find the class representatives mj.
**The test feature vectors are then classified using Minimum Distance, and the percent correct classification of the classifier evaluated.
The images of objects to be classified:



(a) (b) (c)
images of kwekwek (a), pillows (b), and squidballs (c)
Pattern recognition is basically deciding whether a given feature vector (an ordered set of a quantifiable property, features that make up a pattern, such as color, shape, size, etc.) belongs to one of several classes (a set of patterns that share a common property).
Procedure:
**A set of objects are assembled that may be classified into 2 to 5 classes, with 10 samples for each class. Half serves as a training set, while the other half serves as a test set.
[Photo]
**Images of these objects are captured while features are chosen and extracted from them. These features are then separated into test feature vectors and training feature vectors.
Here we choose:
**The training feature vectors are then used to find the class representatives mj.
Letting wj (where j=1,2,3...W) be a set of classes and W be the total number of classes. The class representative is defined as the mean feature vector and obtained using the following equation:

where xj is the set of all feature vectors and Nj is the number of samples of class wj
**The test feature vectors are then classified using Minimum Distance, and the percent correct classification of the classifier evaluated.
A way of determining class membership is classifying an unknown feature vector x (in this case our test feature vectors) into the class whose mean or representative it is nearest to. Minimum Distance is then computed using the equation (derived from the Eucledian distance):
x is then classified into the index with the smallest distance.
where j=1,2,3,...W
The images of objects to be classified:



(a) (b) (c)
images of kwekwek (a), pillows (b), and squidballs (c)
The objects are first segmented manually so that only one object remains per image (gimp). then color image segmentation (activity 16) was used to isolate the region of interest (from this step we obtain the R G B values of the objects to use as features).
Then using a simple code:
im=imread('kwek1.jpg');
kwek1b=im2bw(im);
[x,y] = follow(kwek1b);
wid= max(x) - min(x);
hgt= max(y) - min(x)
wh = wid/hgt
we obtain the ratio of the width of the object over the height (easier than obtaining area) as a last feature.
Then the first equation above is applied to the obtained values to obtain the class representative, the results of which are given below.
Applying the second equation mentioned above to obtain the minimum distance:
 table where smallest values indicate classification
table where smallest values indicate classification
Then using a simple code:
im=imread('kwek1.jpg');
kwek1b=im2bw(im);
[x,y] = follow(kwek1b);
wid= max(x) - min(x);
hgt= max(y) - min(x)
wh = wid/hgt
we obtain the ratio of the width of the object over the height (easier than obtaining area) as a last feature.
Then the first equation above is applied to the obtained values to obtain the class representative, the results of which are given below.
Applying the second equation mentioned above to obtain the minimum distance:
 table where smallest values indicate classification
table where smallest values indicate classificationas we can see above, all objects from the test set were classified correctly, although the minimum distance values were close to each other.
i give myself a grade of 10 for this activity. the classification was 100% effective.
thank you to julie ting from whom i obtained the images, since i was absent that day. thank you also to jeric for explaining the concept to me.
i give myself a grade of 10 for this activity. the classification was 100% effective.
thank you to julie ting from whom i obtained the images, since i was absent that day. thank you also to jeric for explaining the concept to me.

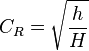



![[ncc.jpg]](http://4.bp.blogspot.com/_6ZpN6X5LZPw/SL0FXYODUJI/AAAAAAAAAhw/pGj2mmL1yDk/s1600/ncc.jpg)


![[rgcc.jpg]](http://3.bp.blogspot.com/_6ZpN6X5LZPw/SL0HAiF92HI/AAAAAAAAAh4/_TufRbVLtT4/s1600/rgcc.jpg)

